


Next: 2.1.3 Polyatomic Oscillators
Up: 2.1 General Theory of
Previous: 2.1.1 Atomic Oscillators
Contents
2.1.2 Quantum Oscillators
Application of quantum mechanics to the diatomic system leads to several
important conclusions:
- The system cannot be observed at any random vibrational energy between
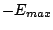 and
and 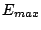 as depicted in Section 2.1.1.
as depicted in Section 2.1.1.
- The vibrational energy of a given state is related to the classical
frequency of oscillation.
where v is the vibrational quantum number, h is Planck's
constant and 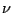 is the classical frequency of oscillation. In
other words, the possible energies for a system are discrete, as given
by states described by the vibrational quantum number v.
is the classical frequency of oscillation. In
other words, the possible energies for a system are discrete, as given
by states described by the vibrational quantum number v.
- The energy between two discrete states is also discrete. The
energy required to change states corresponds to the discrete energy
between states.
- The vibrational state can be changed by absorption (or emission) of
infrared light, provided:
- The light frequency is equal to the frequency of the equivalent classical
oscillator.
- The transition between the states is allowed (See Section2.1.4).



Next: 2.1.3 Polyatomic Oscillators
Up: 2.1 General Theory of
Previous: 2.1.1 Atomic Oscillators
Contents
John S. Riley, DSB Scientific Consulting